Diffusion-thermo effects on MHD free convective radiative and chemically reactive boundary layer flow through a porous medium over a vertical plate

Prakash, J.; Durga Prasad, P.; Kiran Kumar, R. V. M. S. S.; Varma, S. V. K.

doi:10.22061/jcarme.2016.429

Document Type : Research Paper

Authors

¹ Department of Mathematics, University of Botswana, Private Bag 0022, Gaborone, Botswana

² Departmentof Mathematics, Sri Venkateswara University, Tirupati – 517502, A. P., India

https://doi.org/10.22061/jcarme.2016.429

Abstract

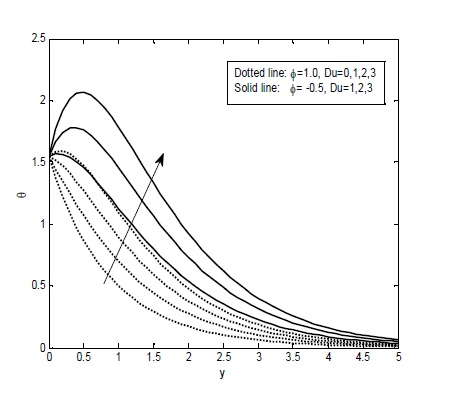
The main purpose of this work is to investigate the porous medium and diffusion-thermo effects on unsteady combined convection magneto hydrodynamics boundary layer flow of viscous electrically conducting fluid over a vertical permeable surface embedded in a high porous medium, in the presence of first order chemical reaction and thermal radiation. The slip boundary condition is applied at the porous interface. A uniform Magnetic field is applied normal to the direction of the fluid flow. The non-linear coupled partial differential equation are solved by perturbation method and obtained the expressions for concentration, temperature and velocity fields. The rate of mass transfer in terms of Sherwood number , the rate of heat transfer in terms of Nusselt number and the Skin friction coefficient are also derived. The Profiles of fluid flow quantities for various values of physical parameters are presented and analyzed. Profiles of fluid flow quantities for various values of physical parameters are presented and analyzed.

Keywords

20.1001.1.22287922.2016.5.2.3.9

Main Subjects

References

[1] R. S. Rath, and D. N. Parida, “Magneto-hydrodynamic free convection in the boundary layer due to oscillation in the wall temperature”, Wear, Vol. 78, No. 1, pp. 305-314, (1982).

[2] A. Raptis, G. Tzivanidis, and N.Kafusias, “Free convection and mass transfer flow through a porous medium bounded by an infinite vertical limiting surface with constant suction”, Letters in Heat and Mass Transfer, Vol. 8, No. 1, pp. 417-424, (1981).

[3] B. K. Jha, and R.Prasad, “MHD free-convection and mass transfer flow through a porous medium with heat source”, Astrophysics and Space Science, Vol. 18, No. 1, pp. 117-123, (1991).

[4] K.Yamamoto, and N. Iwamura, “Flow with convective acceleration through a porous Medium”, J. Eng. Math, Vol. 10, No. 1, pp .41-54, (1976).

[5] B. Gebhart, and L. Pera, “The nature of vertical natural convection flows resultingfrom thecombined buoyancy effects of thermal and mass diffusion”, Int. J. Heat and Mass Transfer,Vol. 14,No. 12, pp. 2025-2050, (1971).

[6] D. Pal and B. Talukdar, “Perturbation Analysis of unsteady magneto hydro- dynamic convective heat and mass transfer in a boundary layer slip flow past a vertical permeable plate with thermal radiation and chemical reaction”, Commun Nonlinear Sci Number Simulant, Vol. 15, No. 7, pp. 1813-1830, (2010).

[7] D. Nield and A. Bejan, “Convection in porous media”, 2^nd edition Springer, Wiley, New York, pp. 62-75, (1995).

[8] P. Cheng, “Heat transfer in geothermal system”, Adv Heat Transfer,Vol. 4, No. 1, pp. 1-105, (1978).

[9] N. Rudraiah, “Flow through and past porous media, ”Encyclopediaof Fluid Mechanics, Gulf Publ. Vol. 5, pp. 567-647, (1986).

[10] N. Rudraiah, D. Pal, and I. N. Shivakumara, “Effect of slip and magnetic field on composite systems”. Fluid Dyn. Res., Vol. 4, No.4, pp. 255-270, (1988).

[11] A. Apelblat, “Mass transfer with a chemical reaction of the first order: AnalyticalSolutions”, The Chemical Engineering Journal Vol. 19, No. 1, pp. 19-37, (1980).

[12] U. N. Das, R. K. Deka and V. M. Soundalgekar, “Effects of Mass transfer on flow past an impulsively started infinite vertical plate with constant heat flux and chemicalreaction”, Forschung imIngenieurwesen, Vol. 60, No. 10, pp. 284-287, (1994).

[13] P. L. Chambre and J. D. Young, “On the diffusion of a chemically reactive species in a laminar boundary layer flow”, The Physics of Fluids, Vol. 1, pp. 48-54, (1958).

[14] W. G. England, and A. F. Emery, “Thermal radiation effects on the laminar free convection boundary layer of an absorbing gas”, Journal of Heat Trans, Vol. 91, No. 1, pp. 37-44,(1969).

[15] V. M. Soundalgekar, and H. S. Takhar, “Radiation effects on free convection flow past a semi-verticalplate”, Modeling Measurement and Control, Vol. 51,pp. 31-40, (1993).

[16] A. Raptis, and C. Peridikis, “Radiation and free convection flow past a moving plate”, International Journal ofApplied Mechanicsand Engineering, Vol. 4, No. 4, pp. 817-821, (1999).

[17] F. S. Ibrahim, A. M. Elaiw and A. A. Bakr, “Effects of the chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi-infinite vertical permeable moving plate with heat source and suction”, CommunicationsinNonlinearScienceandNumericalSimulation, Vol. 13, No. 6, pp. 1056-1066, (2008).

[18] Z. Dursunkaya, and W. M. Worek, “Diffusion–thermo and thermal-diffusion effects in transient and steady natural convection from vertical surface”, International Journal of Heatand Mass Transfer, Vol. 35, No. 8, pp. 2060-2065, (1992).

[19] M. Anghel, H. S. Takhar and I. Pop, “Dufour and Soret effects on free convection boundary layer over a vertical surface embedded in a porous medium”,StudiaUniversitatisBabes-Bolyai, Mathematica Vol. 45, No. 4,pp. 11-21, (2000).

[20] A. Postelnicu, “Influence of a magnetic field on heat and mass transfer by natural convectionfrom vertical surfaces in porous media considering Soret and Dufoureffects”, International Journal of Heat and Mass Transfer, Vol. 47, No. 6, pp. 1467-1472, (2004).

[21] A. J. Chamkha, “Unsteady MHD convective heat and mass transfer past a semi-infinite vertical permeable moving plate with heat absorption”, International Journal of Engineering Sciences,Vol. 42, No. 2, pp. 217-230, (2004).

[22] A. J. Chamkha, “MHD flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction”, Int. Comm. Heat Mass Transfer, Vol. 30, No. 3, pp. 413-422, (2003).

[23] R. A. Mohamed, “Double-diffusive convection radiation interaction on unsteady MHD flow over a vertical moving porous plate with heat generation and Soret effects”, Appl. Math. Sci., Vol. 3, No. 13, pp. 629-651, (2009).

[24] R. Muthucumaraswamy and B. Janakiraman, “MHD and radiation effects on moving isothermalvertical plate with variable mass diffusion”, Theo. Appl. Mech., Vol. 33, No.1, pp. 17-29, (2006).

[25] V. Rajesh and S. V. K. Varma, “Thermal diffusion and radiation effects on MHD flow past an impulsively started infinite vertical plate with variable temperature and mass diffusion”, JP J. Heat and Mass Transfer, Vol. 3,No. 1, pp. 17-39, (2009).

[26] A. G .Vijaya Kumar and S. V. K. Varma, “Thermal radiation and mass transfer effects on MHD flow past an impulsively started exponentially accelerated vertical plate with variable temperature and mass diffusion”, Far East J. Appl. Math., Vol. 55,No. 2, pp. 93-115, (2011).

[27] R. A. Raptis, C. Perdikis and A. Leontitsis, “Effects of radiation in an optically thin gray gas flowing past a vertical infinite plate in the presence of magnetic field”, Heat and Mass Transfer, Vol. 39, pp. 771-773, (2003).

[28] A. Orhan and K. Ahmad,“Radiation effect on MHD mixed convection flow about a permeable vertical plate”, Heat and Mass Transfer, Vol. 45,No. 2, pp. 239-246, (2008).

[29] S. Ahmad, “ Inclined magnetic field with radiating fluid over a porous vertical plate: Analytical study”, Journal Naval Arch. Marine Engineering, Vol. 7, No. 2, pp. 61-72, (2010).

[30] E. R. G. Eckert, and R. M. Drake, “Analysis of Heat and Mass Transfer”, M.C.Graw-Hill, New- York, (1972).

[31] J. Prakash, D. Bhanumathi, A. G. Vijaya Kumar “Radiation effects on unsteady MHD flow through porous medium past an impulsively started infinite vertical plate with variable temperature and mass diffusion”, Trans. Porous. Med. Vol. 96, No. 1,pp. 135-151, (2013).

[32] A. C. Cogley, W. G. Vincent and S. E. Giles, “Differential approximation to radiative heat transfer in a non-grey gas near equilibrium”, American Institute of Aeronautics and Astronautics, Vol. 6, No. 3, pp. 551-553, (1968).

[33] Y. J. Kim, “Unsteady MHD convective heat transfer past a semi-infinite vertical moving plate with variable suction”, International Journal of Engineering Sciences, Vol. 38, No. 8, pp. 833-845, (2000).

Name *

Email Address *

Affiliation *

Comments *

Security Code *

Journal of Computational & Applied Research in Mechanical Engineering (JCARME)

Diffusion-thermo effects on MHD free convective radiative and chemically reactive boundary layer flow through a porous medium over a vertical plate

References

References

Send comment about this article

Volume 5, Issue 2
June 2016
Pages 111-126

Diffusion-thermo effects on MHD free convective radiative and chemically reactive boundary layer flow through a porous medium over a vertical plate

References

References

Send comment about this article

Volume 5, Issue 2June 2016Pages 111-126

Volume 5, Issue 2
June 2016
Pages 111-126